Validation of prognostic models: challenges and opportunities

Multivariable prognostic models combine several characteristics to provide predictions for individual patients. Prognostic models can be applied in research and clinical practice, for instance to assist clinicians with decisions regarding treatment choices or informing patients and family members on prognosis (1). Before application in clinical practice, prognostic models should be validated to judge their generalizability. Although guidelines have been proposed to improve development and reporting of prognostic models, a majority of the published models is not thoroughly validated (1,2). In this viewpoint, we focus on design and analysis of validation studies for prognostic models. For illustration, we consider the validation of the International Mission for Prognosis and Analysis of Clinical Trials in Traumatic Brain Injury (IMPACT) prognostic models for patients with moderate and severe traumatic brain injury. These models combine clinical, radiological and laboratory admission characteristics to predict risk of mortality and unfavorable outcome (3). A second example is on computed tomography (CT) decision rules in patients with minor head injury (4).

Model development

Development of a prognostic model needs to consider various steps, such as the specification and coding of predictors for the model, and how to estimate the model parameters (5). Regression modeling is the most common approach, while machine learning techniques are gaining interest. Both regression and machine learning methods provide predictions for individual patients. It is important to evaluate the quality of the predictions for the derivation cohort (internal validation) as well as for new settings that may differ from the derivation cohort (external validation) (5,6).

Internal validation

Apparent validation implies assessment of model performance directly in the derivation cohort. This approach yields an optimistic estimate of model performance, because the regression coefficients are optimized for the derivation cohort (5). Split-sample validation entails random splitting of the derivation cohort into a development and validation sample. This is a standard but inefficient procedure, and is therefore not recommended (6). Cross-validation and bootstrap resampling are more reliable and desirable methods for internal validation. Cross-validation comprises model development on a part of the derivation cohort, and validation on the rest of the sample. This process is repeated until all patients have been used for model validation, and model performance is estimated over all validations (5). A 10-fold cross-validation uses 90% of the derivation sample for development with validation at 10%; repeated 10 times. Bootstrap resampling indicates drawing random samples with replacement from the derivation cohort, with sample size equal to that of the original cohort. A model is constructed in the bootstrap sample, and its performance is evaluated both in the bootstrap sample and the original cohort. The difference indicates the optimism in performance (5). This optimism is subtracted from the apparent performance to indicate the expected model performance for future patients similar to the derivation cohort. At least 100 samples should be drawn to obtain stable estimates.

External validation

External validation relates to the generalizability and transportability of the prognostic model to another population (1,5). For example, the IMPACT models were validated in the Corticosteroid Randomisation after Significant Head Injury (CRASH) trial—an independent and more recent cohort (3). An elegant variant of cross-validation can also be applied if data from multiple studies are analyzed: validation by leaving out all of the included studies once (3,7).

Performance measures

The classic measures to express model performance are discrimination and calibration. Discrimination refers to the ability of the prognostic model to distinguish between high and low risk patients, and is commonly quantified with the concordance statistic (C-statistic, equal to the area under the receiver operating characteristic curve, AUC). At internal validation, optimism in the C-statistic of the IMPACT models was minimal according to a bootstrap resampling procedure. This is explained by the large sample size (>5,000 patients in all analyses). At cross-validation by study, C-statistics ranged between 0.66 and 0.87, with slightly better performance with increasing model complexity. At validation in the CRASH trial, the C-statistics for the IMPACT core and extended models ranged from 0.78 to 0.83 (3). Note that the discriminative ability of a model at external validation is influenced by differences in case-mix between the derivation and validation cohort. Discriminating high from low risk is more feasible in a heterogeneous population (e.g., an observational study) than in a homogeneous population (e.g., a randomized trial). Indeed, higher C-statistics were found when validating the IMPACT models in less selected cohorts rather than in a randomized controlled trial with strict inclusion criteria (8).

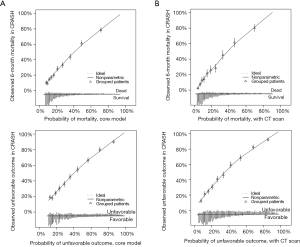
Calibration indicates the agreement between observed outcomes and predicted probabilities. Calibration may be assessed graphically in a calibration graph (Figure 1A,B). Ideally, we observe a 45 degree line with calibration slope 1 and intercept 0. Calibration is less relevant at internal validation, because any model provides on average correct predictions for the derivation cohort. At external validation, the IMPACT models showed some miscalibration, with systematic underestimation of the risk for mortality and unfavorable outcome (Figure 1A,B) (3). Such systematic miscalibration may be attributed to differences in predictors that were not included in the proposed model, e.g., differences in treatment. In the current literature on prognostic models, the importance of model calibration is often undervalued. Adequate model calibration is however crucial for adequately informing patients about their risks, and for decision support (9).

Figure 1 Calibration plots for the (A) International Mission for Prognosis and Analysis of Clinical Trials in Traumatic Brain Injury (IMPACT) core model (including age, motor score and pupillary activity) and (B) IMPACT computed tomography (CT) model (extending the core model with CT characteristics and history of hypoxia and hypotension). Mortality and unfavorable outcome were evaluated in the Corticosteroid Randomisation after Significant Head Injury (CRASH) trial. The distribution of predicted probabilities is shown at the bottom of the graphs, stratified by outcome. Reprinted with permission from Steyerberg et al. (3).

Decision support

Some prognostic models explicitly aim to support clinical decision making. For these models, an additional decision-analytic evaluation is required, beyond discrimination and calibration. An example of such an evaluation is provided for the validation of CT decision rules in minor head injury (4). These rules are used to identify patients with minor head injury at risk of intracranial complications who need a CT. In this decision problem, the need to identify patients with a clinically relevant intracranial abnormality (true positives) is weighed against the wish to avoid unnecessary CTs (false positives). A decision-analytic measure that can be used to express this balance is net benefit (NB). NB is calculated as a weighted sum of true and false positive classification: (true positives – weight × false positives) / total number of patients (4,5,10). The weight is defined clinically by balancing the relative importance of the benefits and harms. To facilitate interpretation of NB and judge clinical utility of the model, a ‘decision curve’ can be plotted with a range of risk thresholds. The NB of a CT decision rule needs to be better than the reference strategies “no scanning” and “scanning all patients” (10).

Conclusions

Validation of prognostic models is a crucial step before we start implementation in clinical practice. Models should be internally and especially externally validated to obtain reliable estimates of model performance, including assessments of discrimination and calibration. Decision-analytic evaluation is important to identify models that aim to improve clinical decision making. Finally, variation in model performance is commonly observed across different settings when a prognostic model is externally validated extensively. Therefore, validated prognostic models should be applied in addition to clinical experience and only if the model is expected to be applicable to the specific setting and patient.

Acknowledgements

None.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Steyerberg EW, Moons KG, van der Windt DA, et al. Prognosis Research Strategy (PROGRESS) 3: prognostic model research. PLoS Med 2013;10. [Crossref] [PubMed]
2. Moons KG, Altman DG, Reitsma JB, et al. Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med 2015;162:W1-73. [Crossref] [PubMed]
3. Steyerberg EW, Mushkudiani N, Perel P, et al. Predicting outcome after traumatic brain injury: development and international validation of prognostic scores based on admission characteristics. PLoS Med 2008;5:e165; discussion e165.
4. Foks KA, van den Brand CL, Lingsma HF, et al. External validation of computed tomography decision rules for minor head injury: prospective, multicentre cohort study in the Netherlands. BMJ 2018;362:k3527. [Crossref] [PubMed]
5. Steyerberg EW. Clinical prediction models: a practical approach to development, validation and updating. New York: Springer; 2009.
6. Steyerberg EW, Harrell FE Jr, Borsboom GJ, et al. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol 2001;54:774-81. [Crossref] [PubMed]
7. Riley RD, Ensor J, Snell KI, et al. External validation of clinical prediction models using big datasets from e-health records or IPD meta-analysis: opportunities and challenges. BMJ 2016;353:i3140. [Crossref] [PubMed]
8. Roozenbeek B, Lingsma HF, Lecky FE, et al. Prediction of outcome after moderate and severe traumatic brain injury: External validation of the International Mission on Prognosis and Analysis of Clinical Trials (IMPACT) and Corticoid Randomisation after Significant Head injury (CRASH) prognostic models. Critical Care Medicine 2012;40:1609-17. [Crossref] [PubMed]
9. Van Calster B, Vickers AJ. Calibration of risk prediction models: impact on decision-analytic performance. Med Decis Making 2015;35:162-9. [Crossref] [PubMed]
10. Vickers AJ, Van Calster B, Steyerberg EW. Net benefit approaches to the evaluation of prediction models, molecular markers, and diagnostic tests. BMJ 2016;352:i6. [Crossref] [PubMed]