A review of modeling methods for predicting in-hospital mortality of patients in intensive care unit

Background

ICU wards have significantly grown since it was established in the 1960s in the United States and they are now routinely provided to the general public worldwide. Although ICU are equipped with advanced monitoring devices or high ratio of medical resources, the mortality for patients in ICU is still high (1). Moreover, decisions in the ICU are frequently made in the setting of a high degree of uncertainty. In fact, even experienced ICU workers are confused in estimating the risk or probability of death for patients only by their experiences (2). Therefore, a data-based prediction tool is highly necessary and considerable efforts have been invested into this field. Several severity scoring models, now called risk prediction model, which can determine illness severity and predict patient mortality by integrating a variety of information have been developed. Among these scoring models, acute physiology and chronic health evaluation (APACHE I–IV) (2-5), simplified acute physiology score (SAPS I–III) (6-8), and mortality probability models (MPM I–III) (1,9,10) are the most popular models. Although each type of model has been updated more than once, the external validation indicates that all those existing models are still limited if they are applied in the population in which the case-mix is distinct from the population where it was originally developed.

With the development of information technology, the use of electronic health records (EHRs) has increased dramatically and make large amounts of clinical data kept in digitization, which not only facilitate billing and patient care but also provides opportunities for research, including developing and refining and validating risk prediction model (11-13). Over the past 10 years, at least 200 studies have been published creating prediction models using local EHR data. Overall, it is convincible that the locally developed models present more excellent performance compared to the standard severity scoring systems even if the former have not been widely validated (14). Besides, the locally developed models can be updated and improved quickly as every patient data collected into EHRs, which is superior for APACHE or SAPS with more than 5 years update interval. Third, every severity scoring systems has fixed variables and coefficients, which may be impractical for primary hospitals that are not able to collect so much clinical information. However, the locally developed models can provide investigators with sufficient freedom and flexibility to devise their customized models according their available data.

Therefore, this review attempts to introduce the essential concepts, procedures and methods for the investigators who want to develop an in-hospital mortality prediction model based on local EHRs database.

Predictor selection

Predictor (variable) selection is very important in both statistical modeling and machine learning modeling. The objective of the predictor selection is to find the variables which are the most relevant for prediction and removes the predictors which are non-informative or redundant for prediction. In most cases, the accuracy of the model is improved when the selected variables are used. Meanwhile, valid predictor selection can save the cost of data collection (15).

In the field of mortality prediction for ICU patients, the clinical experience and knowledge in the literature are two important foundations for identification of variables that might be potential predictors of the outcome. Current viewpoints support that physiological variables included in severity scoring models are key determinants of mortality for ICU patients. In addition, age, comorbidity, admission type, patients’ location prior to admission, diagnostic disease category, and even treatment factors in ICUs have also been demonstrated to be useful in improving model performance (4,5). For example, APACHE-IV (5), the newest version of APACHE, has included therapy information in its mortality prediction equation. Furthermore, some biomarkers (gene symbols) were proved to have predictive strength for poor outcomes (16,17). Wong et al. used five candidate biomarkers variables to derive a decision tree (DT) model and found that it reliably estimates the death risk in adults with septic shock (18-20). However, most biomarkers are not routinely measured in ICU and not covered by Medicare.

Ideal risk factors should be clinically relevant and mathematically related to the outcome of interest (21). After the candidate variables are chosen on the basis of clinical experience or widely used scoring models, the data-driven screening techniques are also required to filter variables. These techniques are generally divided into three categories: univariate analysis, multivariate analysis, and built-in approach. Univariate analysis is used to determine whether or not a plausible relationship exists between the predictors and the outcome by evaluating every predictor individually. Only predictors with important relationships would then be included in a model. Commonly, Pearson’s chi-square or Fisher exact test is utilized for categorical variables, while t-test or Mann-Whitney U test is adopted for continuous variables (22). However, redundant (i.e., highly-correlated) predictors may be selected only by univariate analysis. Besides, multivariate analysis approaches, including forward selection (23), backward selection (7), and stepwise regression (24), are also popular by investigators. Although no sufficient theory assures that backward selection is better than other selection methods, it is highly recommended by most statisticians (25-28). Lastly, different from the first two analysis methods, built-in approaches perform variable selection during model construction like tree- or rule-based models (18) and the so-called Lasso model (least absolute shrinkage and selection operator) (29-31). Overall, reliable subsets of predictors can be ensured by combining clinical experiences and statistical techniques.

Modeling methods

In ICUs, mortality prediction rules can be developed on the basis of clinical experiences of physicians or using a series of methods, including statistical analysis and machine learning techniques (3,32,33). In 1981, the first version of the APACHE scoring system was published (2). It was entirely based on the subjective evaluations of an expert panel. Afterward, statistical analysis, such as logistic regression (LR), has been the mainstream modeling method for over 30 years. However, in the era of big data, machine learning techniques are becoming a potential alternative to classical statistical techniques (13,25-28,34). In this section, we will discuss some detailed issues regarding the adoption of these methods for the prediction of mortality in the ICU setting.

LR

LR is the current standard for prognostic modeling and is best known by clinicians due to its simplicity and ability to make inferential statements about model terms. For example, the coefficients can be converted into corresponding odds ratios which indicate the strength of association between a predictor and an outcome variable. However, this method shows obvious shortcomings. First, it imposes linear constrains on the relationship between the predictor variables and corresponding outcomes. Although fractional polynomials (FPs) have been advocated recently to model non-linear relationships, it does require the user to identify effective representations of the predictor data that yield the best performance (35,36). Second, collinearity that the predictors are strongly correlated with each other hampers reliable estimation of regression coefficients of the correlated variables in LR model (37). Third, modeling high-level interaction are difficult even unfeasible for LR model (38).

The most common severity scoring models in ICU are based on LR, but obvious diversities are still observed in model derivation. For example, both APACHE (2-5) and SAPS (6-8) used an indirect modeling strategy wherein a summary score of disease severity is generated first before the severity score together with other essential data are used to estimate the survival probability. Unlike these approaches, all MPM versions (9,10) use LR directly to construct models based on available data. In general, the indirect LR architecture has the advantage of being less covariate and thus may minimize overfitting. Meanwhile, the direct LR architecture can extract information sufficiently from predictor variables, and thus it can potentially produce a better fitting LR model.

Artificial neural networks (ANNs)

ANNs comprises a large class of models that can identify autonomously and model implicit nonlinear relations between the outcome and predictor variables (39). In principle, ANNs can approximate any continuous functional mapping with arbitrary precision if it includes sufficient hidden nodes (40). Compared to LR, one notable advantage of neural network analysis is that there are few assumptions that must be verified before the models can be constructed. Besides, ANNs allow the inclusion of a large number of variables without the consideration of collinearity. Baxt et al. (41) suggested that neural nets are particularly well suited to modeling complex clinical scenarios like ICU setting.

The feed-forward multilayer perceptron neural network is the most frequently used ANNs for the mortality prediction in ICU. This type of ANNs is characterized by three features, namely, network architecture, activation function, and weight learning algorithm. Figure 1 shows a diagram of the model architecture of a typical ANNs, which consists of three artificial neuron layers: input, hidden, and output layers. The input layer receives the values of the predictor variables (e.g., age, heart rate, and body temperature), and the output layer provides the predicted outcome (death or survival). Each neuron in the hidden and output layers takes the sum of values from each input value multiplied by the relevant weight. Then, the activation function (also known as squashing function) is applied to calculate the output result. Notably, although several algorithms are available through which all the weights in the net can be trained, ANNs have not been studied thoroughly in medical research area until the rediscovery of the backpropagation (BP) algorithm (42).

Figure 1 Structure of a typical three-layer feed forward multilayer perceptron ANNs. ANNs, artificial neural networks.

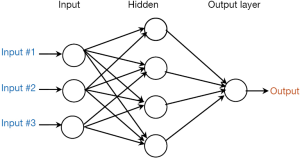
When we modeling mortality using ANNs, some caution should be paid. First, the number of nodes and hidden layer should be determined. Dybowski et al. (43) configured their ANNs model by means of a genetic algorithm that can automatically search optimal neural net configuration. They found that this algorithm can formulate relatively accurate hospital mortality prediction compared with LR model. Meanwhile, Kim et al. (13) used the exhaustive prune method, which can search the space of all possible models to determine the best one. However, most researchers “tune” the internal structure of the neural net through the trial-and-error method or merely subjective experience (32,44-46). Second, the training algorithm that can obtain the net weight (parameter) should be identified. The original BP algorithm is the most well-known learning algorithm. However, it is extremely slow for most applications (47). To address this issue, Xia et al. (48) investigated variants of the BP algorithm, such as the Bayesian regulation, conjugate gradient, and Levenberg-Marquardt BP algorithms. They concluded that the Levenberg-Marquardt BP algorithm is the best with respect to speed. Silva et al. (24) then proposed the use of resilient propagation, which is an enhanced version of the BP algorithm to improve training efficiency and reduce the computational resources. Third, determining an appropriate stopping rule is crucial, because overtraining can result in overfitting and poor generalization capabilities, while undertraining decrease the accuracy. Thus, a simple approach is to stop after a certain iteration time, which is normally set using domain knowledge or experience (45). Jaimes et al. (49) used a more dynamic technique where an error measurement reaches a threshold. However, most modelers did not report the criterion of stopping (50,51).

The lack of interpretability at the level of individual predictors is one of the most criticized features of ANNs (52). But if the model will only be utilized for prediction, this limitation may be less important.

DT

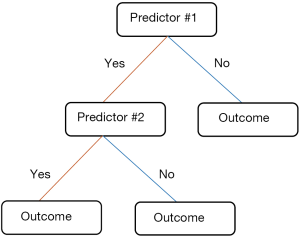
DT is a group of tree-based classification methods that have been successfully used in several healthcare applications (27,53-57). An advantage of a tree is its simple presentation of the decision rules which has garnered considerable acceptance from professionals in clinical practice (58). Another advantage may be that interaction effects are naturally incorporated in a tree, while a standard LR model usually starts with main effects. If the optimal models not only must provide an accurate prediction but also improve our understanding for the disease mechanism, DT appears to deliver the best trade-off between accuracy and interpretability.

Figure 2 presents a basic construct about DT that contains nodes and lines. Each tree conjunction is called a node. Beginning with the parent node, the tree is divided into a series of child nodes. Subsequently, a terminal node is produced at the end of each tree branch. Two adjacent nodes are linked by a line segment, which indicates the different node values. Although the basic tree structure of DT is similar, its partitioning rules are different. For example, Salzberg et al. (59) choose C4.5 algorithm to develop prognostic model (58), which determines the best splits of nodes based on entropy-based criterion called “information gain ratio”. Wong et al. (18) adopted classification and regression trees to predict the 28-day mortality. This method applied the so-called Gini index as their branching criterion. Although a lot of more complex splitting criteria have been developed (60-63) they are uncommon in medical studies. The published studies have argued that these criteria have slight influence on prediction model performance and no single splitting criterion is proven to be absolutely better than the another (64). Similar to ANNs, DT requires modification to prevent overfitting. Trujillano et al. (28) applied an intuitive approach through predetermination of the maximum number of terminal nodes. Post-pruning is another approach that initially grows an overly trained tree, and then removes the branches that do not provide valuable information. In general, post-pruning is relatively objective compared with other approaches (15,64,65).

Figure 2 Structure of a typical DT. DT, decision tree.

Although DT can be converted to a set of rules, this sort of representation is considered as too complicated to comprehensible when facing too much predictors (66).

Support vector machine (SVM)

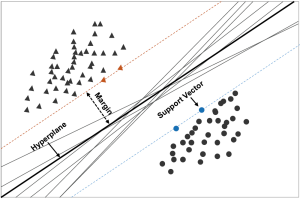
SVM, which was first developed in the mid-1990s by Cortes et al. (67), has undergone evolution and became the most flexible and effective data mining tool after Boser (68) applied the kernel trick to maximum-margin hyperplanes. The SVM often provides better results compared with other techniques (69).

Figure 3 containing an infinite number of classification boundaries provides a visual description of SVM. All these boundaries perfectly classify the data points but SVM can help to find the best one which maximize distance between the classification boundaries and the closest point by introducing appropriate kernel functions. In SVM terminology, the optimal classification boundary is called hyperplanes, the closest point is designated as the support vector, and the distance between the hyperplane and support vectors is termed the margin. and DT. With the goal of predicting mortality risk of cardiovascular patients admitted in ICUs, Moridani et al. (70) selected radial basis as kernel function, and concluded that SVM performs better than ANNs. Houthooft et al. (71) used eight types of machine learning models to predict patient survival and ICU length of stay. Their results suggested that SVM attained the best results in terms of patient mortality prediction. Kim et al. (13) also did a similar comparison, and obtained similar results. Furthermore, Luaces et al. (72) demonstrated that SVM exhibits better performance compared with APACHE-III when the number of patients for training was higher than 500.

Figure 3 Structure of a typical SVM. SVM, support vector machine.

SVM has been extensively applied in genetics, proteomics, molecular biology, bioinformatics, and cancer research (70,71), but it is rarely used to predict mortality in ICU settings compared with LR, ANNs for the reason that SVM refer to too much sophisticated mathematical knowledge and computer skill and most studies in medicine only reported the model performance and omitted the details of modeling.

Performance evaluation measures

We briefly consider some of the more commonly used performance measures in medicine from the properties of discrimination and calibration (73), without intending to be comprehensive.

Discrimination evaluate the ability of the model to distinguish patients who survived from patients who died and can be qualified through several measures, such as sensitivity, specificity and area under the receiver operator characteristic (ROC) curve (74,75). As the most authoritative and comprehensive measure (76), area under the ROC curves with 1.0 and 0.5 values indicate perfect and random discriminations. this measure was found in the majority of literature about mortality prediction, as shown in Table 1.

Table 1 Area under the ROC curves in many studies
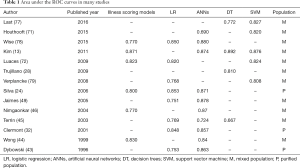
Full table

In addition, the calibration describes the consistency between the estimated probabilities of a model and the observed probabilities over the entire range, which is extremely useful when the models are applied for confounder adjustment in nonrandomized and observational research or for case-mix adjustment for benchmarking ICU performance (1,80). Hosmer-Lemeshow (HL) goodness-of-fit test is the most frequent used method to evaluate calibration. HL statistics with a small value and corresponding high P value suggests good calibration (81). Moreover, Nagelkerke’s R², Brier’s score, and Cox’s calibration regression are also useful measures for the evaluation of model performance (82-85).

Validation

A model may perform better on training dataset than on another dataset. This situation often occurs in both statistical and machine learning models, particularly when the training dataset is small (86). Thus, internal and external validations are very essential for estimating model performance (87). Internal validation means that the model performance is tested using patients who come from the same population as that for model derivation. In internal validation, randomly splitting the training dataset into two mutually exclusive parts is the most popular approach (79). However, this approach often leads to inaccurate and unstable estimation of model performance. Resampling methods, such as cross validation and bootstrap, have been claimed to be more steady and reliable (25,33,88-90). External validation is executed by using data form other institutions (91,92). Either internal or external validation is very necessary before the model can be used in clinical practice (45,93).

Conclusions

ICUs are data-intensive medical settings which pave the way for the development of mortality prediction models. Traditional risk prediction models, commonly called severity scoring models, have been demonstrated to exhibit moderate accuracy with extremely slow updating processes. A plausible reason is that these scoring models were developed using LR, which is unsuitable for modeling complex systems, especially those of critically ill patients whose disease progressions are highly complicated. The proliferation of detailed electronic medical records and the maturation of machine learning techniques have enabled the processing of massive volumes of data. Theoretically, models based on machine learning techniques seem to be more promising in predicting in-hospital mortality of ICU patients compared with traditional statistical methods (87). Therefore, if accuracy is paramount, then these methods can be considered. Moreover, existing modeling methods use the worst value of each variable collected on the first ICU day to perform model derivation and test while ignoring the temporal nature of the predictor sets. Therefore, future ICU mortality studies must take into account the dynamic characteristics of predictors. Furthermore, combining machine learning methods with survival analysis is more scientific and rational when deriving mortality prediction models for patients in ICUs. In future, this work may be extended to develop a risk prediction system that can facilitate timely care and intervention.

Acknowledgements

Funding: This study is supported by Peking University under Grant No. BMU20160592.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Power GS, Harrison DA. Why try to predict ICU outcomes? Curr Opin Crit Care 2014;20:544-9. [Crossref] [PubMed]
2. Knaus WA, Zimmerman JE, Wagner DP, et al. APACHE-acute physiology and chronic health evaluation: a physiologically based classification system. Crit Care Med 1981;9:591-7. [Crossref] [PubMed]
3. Knaus WA, Draper EA, Wagner DP, et al. APACHE II: a severity of disease classification system. Crit Care Med 1985;13:818-29. [Crossref] [PubMed]
4. Knaus WA, Wagner DP, Draper EA, et al. The APACHE III prognostic system. Risk prediction of hospital mortality for critically ill hospitalized adults. Chest 1991;100:1619-36. [Crossref] [PubMed]
5. Zimmerman JE, Kramer AA, McNair DS, et al. Acute physiology and chronic health evaluation (APACHE) IV: Hospital mortality assessment for today's critically ill patients. Crit Care Med 2006;34:1297-310. [Crossref] [PubMed]
6. Le Gall JR, Lemeshow S, Saulnier F. A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study. JAMA 1993;270:2957-63. [Crossref] [PubMed]
7. Moreno RP, Metnitz PG, Almeida E, et al. SAPS 3--From evaluation of the patient to evaluation of the intensive care unit. Part 2: Development of a prognostic model for hospital mortality at ICU admission. Intensive Care Med 2005;31:1345-55. [Crossref] [PubMed]
8. Metnitz PG, Moreno RP, Almeida E, et al. SAPS 3--From evaluation of the patient to evaluation of the intensive care unit. Part 1: Objectives, methods and cohort description. Intensive Care Med 2005;31:1336-44. [Crossref] [PubMed]
9. Lemeshow S, Teres D, Klar J, et al. Mortality probability models (MPM II) based on an international cohort of intensive care unit patients. JAMA 1993;270:2478-86. [Crossref] [PubMed]
10. Higgins TL, Teres D, Copes W, et al. Updated mortality probability model (MPM-III). Chest 2005;128:348S. [Crossref]
11. Ohno-Machado L, Resnic FS, Matheny ME. Prognosis in critical care. Annu Rev Biomed Eng 2006;8:567-99. [Crossref] [PubMed]
12. Rosenberg AL. Recent innovations in intensive care unit risk-prediction models. Curr Opin Crit Care 2002;8:321-30. [Crossref] [PubMed]
13. Kim S, Kim W, Park RW. A Comparison of intensive care unit mortality prediction models through the use of data mining Techniques. Healthc Inform Res 2011;17:232-43. [Crossref] [PubMed]
14. Rivera-Fernández R, Vázquez-Mata G, Bravo M, et al. The Apache III prognostic system: Customized mortality predictions for Spanish ICU patients. Intensive Care Med 1998;24:574-81. [Crossref] [PubMed]
15. Harper PR. A review and comparison of classification algorithms for medical decision making. Health Policy 2005;71:315-31. [Crossref] [PubMed]
16. Kaplan JM, Wong HR. Biomarker discovery and development in pediatric critical care medicine. Pediatr Crit Care Med 2011;12:165-73. [Crossref] [PubMed]
17. Wong HR. Genome-wide expression profiling in pediatric septic shock. Pediatr Res 2013;73:564-9. [Crossref] [PubMed]
18. Wong HR, Lindsell CJ, Pettilä V, et al. A multibiomarker-based outcome risk stratification model for adult septic shock. Crit Care Med 2014;42:781-9. [Crossref] [PubMed]
19. Wong HR, Cvijanovich NZ, Anas N, et al. Prospective Testing and Redesign of a Temporal Biomarker Based Risk Model for Patients With Septic Shock: Implications for Septic Shock Biology. EBioMedicine 2015;2:2087-93. [Crossref] [PubMed]
20. Alder MN, Lindsell CJ, Wong HR. The pediatric sepsis biomarker risk model: potential implications for sepsis therapy and biology. Expert Rev Anti Infect Ther 2014;12:809-16. [Crossref] [PubMed]
21. Higgins TL. Quantifying risk and benchmarking performance in the adult intensive care unit. J Intensive Care Med 2007;22:141-56. [Crossref] [PubMed]
22. Kilic S. Chi-square test. J Mood Disord 2016;6:180-2. [Crossref]
23. Caicedo W, Paternina A, Pinzón H. Machine learning models for early Dengue Severity Prediction. In: Advances in Artificial Intelligence - IBERAMIA 2016:247-58.
24. Silva A, Cortez P, Santos MF, et al. Mortality assessment in intensive care units via adverse events using artificial neural networks. Artif Intell Med 2006;36:223-34. [Crossref] [PubMed]
25. Johnson AE, Dunkley N, Mayaud L, et al. Patient specific predictions in the intensive care unit using a Bayesian ensemble. Comput Cardiol 2010;2012:249-52.
26. Citi L, Barbieri R. Physionet 2012 challenge: predicting mortality of ICU patients using a cascaded SVM-GLM paradigm. Comput Cardiol 2010;2012:257-60.
27. Johnson AE, Ghassemi MM, Nemati S, et al. Machine learning and decision support in critical care. Proc IEEE Inst Electr Electron Eng 2016;104:444-66.
28. Trujillano J, Badia M, Servia L, et al. Stratification of the severity of critically ill patients with classification trees. BMC Med Res Methodol 2009;9:83. [Crossref] [PubMed]
29. Baalachandran R, Laroche D, Ghazala L, et al. Predictors of Mortality In Patients Admitted To An Intensive Care Unit With Viral Pneumonia. Am J Respir Crit Care Med 2015;191:A1756.
30. Ghassemi M, Pimentel MA, Naumann T, et al. A Multivariate Timeseries Modeling Approach to Severity of Illness Assessment and Forecasting in ICU with Sparse, Heterogeneous Clinical Data. Proc Conf AAAI Artif Intell 2015;2015:446-53.
31. Zhang Z, Hong Y. Development of a novel score for the prediction of hospital mortality in patients with severe sepsis: the use of electronic healthcare records with LASSO regression. Oncotarget 2017;8:49637-45. [PubMed]
32. Clermont G, Angus DC, DiRusso SM, et al. Predicting hospital mortality for patients in the intensive care unit: a comparison of artificial neural networks with logistic regression models. Crit Care Med 2001;29:291-6. [Crossref] [PubMed]
33. Silva I, Moody G, Scott DJ, et al. Predicting In-Hospital Mortality of ICU Patients: The PhysioNet/Computing in Cardiology Challenge 2012. Comput Cardiol 2010;2012:245-8. [PubMed]
34. Ribas VJ, López JC, Ruiz-Sanmartin A, et al. Severe sepsis mortality prediction with relevance vector machines. Conf Proc IEEE Eng Med Biol Soc 2011;2011:100-3.
35. Royston P, Ambler G, Sauerbrei W. The use of fractional polynomials to model continuous risk variables in epidemiology. Int J Epidemiol 1999;28:964-74. [Crossref] [PubMed]
36. Zhang Z. Multivariable fractional polynomial method for regression model. Ann Transl Med 2016;4:174. [Crossref] [PubMed]
37. Menard S. Applied Logistic Regression Analysis (Quantitative Applications in the Social Sciences). 2nd Edition. Sage, 2002.
38. Jaccard J. Interaction Effects in Logistic Regression (Quantitative Applications in the Social Sciences). 1st Edition. Sage, 2001.
39. Zhang Z. Neural networks: further insights into error function, generalized weights and others. Ann Transl Med 2016;4:300. [Crossref] [PubMed]
40. Kotsiantis SB. Supervised machine learning: a review of classification techniques. Informatica 2007;31:249-68.
41. Baxt WG. Complexity, chaos and human physiology: the justification for non-linear neural computational analysis. Cancer Lett 1994;77:85-93. [Crossref] [PubMed]
42. Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. Springer series in statistics. Second Edition. Berlin: Springer, 2001.
43. Dybowski R, Weller P, Chang R, et al. Prediction of outcome in critically ill patients using artificial neural network synthesised by genetic algorithm. Lancet 1996;347:1146-50. [Crossref] [PubMed]
44. Wong LS, Young JD. A comparison of ICU mortality prediction using the APACHE II scoring system and artificial neural networks. Anaesthesia 1999;54:1048-54. [Crossref] [PubMed]
45. Terrin N, Schmid CH, Griffith JL, et al. External validity of predictive models: a comparison of logistic regression, classification trees, and neural networks. J Clin Epidemiol 2003;56:721-9. [Crossref] [PubMed]
46. Nimgaonkar A, Karnad DR, Sudarshan S, et al. Prediction of mortality in an Indian intensive care unit - Comparison between APACHE II and artificial neural networks. Intensive Care Med 2004;30:248-53. [Crossref] [PubMed]
47. Reggia JA. Neural computation in medicine. Artif Intell Med 1993;5:143-57. [Crossref] [PubMed]
48. Xia H, Daley BJ, Petrie A, et al. A Neural Network Model for Mortality Prediction in ICU. Comput Cardiol 2010;2012:261-4.
49. Jaimes F, Farbiarz J, Alvarez D, et al. Comparison between logistic regression and neural networks to predict death in patients with suspected sepsis in the emergency room. Critical Care 2005;9:R150-6. [Crossref] [PubMed]
50. Xia HN, Keeney N, Daley BJ, et al. Prediction of ICU in-hospital mortality using artificial neural networks. ASME 2013 Dynamic Systems and Control Conference; 2013 October 21-23; Palo Alto, California, USA.
51. Churpek MM, Yuen TC, Winslow C, et al. Multicenter comparison of machine learning methods and conventional regression for predicting clinical deterioration on the wards. Crit Care Med 2016;44:368-74. [Crossref] [PubMed]
52. Tu JV. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J Clin Epidemiol 1996;49:1225-31. [Crossref] [PubMed]
53. Celi LA, Galvin S, Davidzon G, et al. A Database-driven Decision Support System: Customized Mortality Prediction. J Pers Med 2012;2:138-48. [Crossref] [PubMed]
54. Puskarich M. A decision tree incorporating biomarkers and patient characteristics estimates mortality risk for adults with septic shock. Evid Based Nurs 2015;18:42. [Crossref] [PubMed]
55. Neumann A, Holstein J, Le Gall JR, et al. Measuring performance in health care: case-mix adjustment by boosted decision trees. Artif Intell Med 2004;32:97-113. [Crossref] [PubMed]
56. Manning T, Sleator RD, Walsh P. Biologically inspired intelligent decision making: a commentary on the use of artificial neural networks in bioinformatics. Bioengineered 2014;5:80-95. [Crossref] [PubMed]
57. Alotaibi NN, Sasi S. Tree-based ensemble models for predicting the ICU transfer of stroke in-patients. 2016 International Conference on Data Science and Engineering (ICDSE); 2016 Aug 23-25; Cochin: IEEE.
58. Quinlan JR. Induction of decision trees. Machine Learning 1986;1:81-106. [Crossref]
59. Salzberg SL. C4.5: Programs for Machine Learning by J. Ross Quinlan. Morgan Kaufmann Publishers, Inc., 1993. Machine Learning 1994;16:235-40. [Crossref]
60. Mehta M, Agrawal R, Rissanen J. SLIQ: A fast scalable classifier for data mining. In: Apers P, Bouzeghoub M, Gardarin G. editors. Advances in Database Technology — EDBT '96. EDBT 1996. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, 1996.
61. Loh WY, Shih YS. Split selection methods for classification trees. Stat Sin 1997;7:815-40.
62. Gehrke J, Ganti V, Ramakrishnan R, et al. BOAT—Optimistic Decision Tree Construction. New York: Assoc Computing Machinery, 1999:169-80.
63. Gehrke J, Ramakrishnan R, Ganti V. RainForest—A Framework for Fast Decision Tree Construction of Large Datasets. Data Min Knowl Discov 2000;4:127-62. [Crossref]
64. Berzal F, Cubero JC, Cuenca F, et al. On the quest for easy-to-understand splitting rules. Data Knowl Eng 2003;44:31-48. [Crossref]
65. Loh WY. Classification and regression trees. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2011;1:14-23. [Crossref]
66. Rokach L, Maimon O. Data mining with decision trees: theory and applications. World Scientific, 2014.
67. Cortes C, Vapnik V. Support-vector networks. Machine Learning 1995;20:273-97. [Crossref]
68. Boser BE, Guyon IM, Vapnik VN. A training algorithm for optimal margin classifiers. Proceeding COLT '92 Proceedings of the fifth annual workshop on Computational learning theory. 1992 July 27-29, Pittsburgh, Pennsylvania, USA. New York: ACM, 1992:144-52.
69. Moguerza JM, Munoz A. Support vector machines with applications. Stat Sci 2006;21:322-36. [Crossref]
70. Moridani MK, Setarehdan SK, Nasrabadi AM, et al. New algorithm of mortality risk prediction for cardiovascular patients admitted in intensive care unit. Int J Clin Exp Med 2015;8:8916-26. [PubMed]
71. Houthooft R, Ruyssinck J, van der Herten J, et al. Predictive modelling of survival and length of stay in critically ill patients using sequential organ failure scores. Artif Intell Med 2015;63:191-207. [Crossref] [PubMed]
72. Luaces O, Taboada F, Albaiceta GM, et al. Predicting the probability of survival in intensive care unit patients from a small number of variables and training examples. Artif Intell Med 2009;45:63-76. [Crossref] [PubMed]
73. Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology 2010;21:128-38. [Crossref] [PubMed]
74. Obuchowski NA. Receiver operating characteristic curves and their use in radiology. Radiology 2003;229:3-8. [Crossref] [PubMed]
75. Harrell FE Jr. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis (Springer Series in Statistics), Second Edition. Springer, 2015.
76. Collins GS, Reitsma JB, Altman DG, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): The TRIPOD statement. Br J Cancer 2015;112:251-9. [Crossref] [PubMed]
77. Last M, Tosas O, Cassarino TG, et al. Evolving classification of intensive care patients from event data. Artif Intell Med 2016;69:22-32. [Crossref] [PubMed]
78. Wise ES, Hocking KM, Brophy CM. Prediction of in-hospital mortality after ruptured abdominal aortic aneurysm repair using an artificial neural network. J Vasc Surg 2015;62:8-15. [Crossref] [PubMed]
79. Verplancke T, Van Looy S, Benoit D, et al. Support vector machine versus logistic regression modeling for prediction of hospital mortality in critically ill patients with haematological malignancies. BMC Med Inform Decis Mak 2008;8:56. [Crossref] [PubMed]
80. Iezzoni LI. Risk Adjustment for Measuring Health Care Outcomes. 3rd edition. Chicago: Health Administration Press, 2003.
81. Hosmer DW, Lemeshow S. Goodness-of-fit test for the multiple logistic regression model. Commun Stat Theory Methods 1980;A10:1043-69. [Crossref]
82. Harrell FE Jr, Califf RM, Pryor DB, et al. Evaluating the yield of medical tests. JAMA 1982;247:2543-6. [Crossref] [PubMed]
83. Kaltoft MK, Nielsen JB, Salkeld G, et al. Enhancing informatics competency under uncertainty at the point of decision: a knowing about knowing vision. Stud Health Technol Inform 2014;205:975-9. [PubMed]
84. Shapiro AR. The evaluation of clinical predictions. N Engl J Med 1977;296:1509-14. [Crossref] [PubMed]
85. Harrison DA, Brady AR, Parry GJ, et al. Recalibration of risk prediction models in a large multicenter cohort of admissions to adult, general critical care units in the United Kingdom. Crit Care Med 2006;34:1378-88. [Crossref] [PubMed]
86. Chatfield C. Model uncertainty, data mining and statistical inference. J R Stat Soc Ser A Stat Soc 1995;158:419-66. [Crossref]
87. Harrell FE Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996;15:361-87. [Crossref] [PubMed]
88. Iwi G, Millard RK, Palmer AM, et al. Bootstrap resampling: a powerful method of assessing confidence intervals for doses from experimental data. Phys Med Biol 1999;44:N55-62.
89. Krajnak M, Xue J, Kaiser W, et al. Combining machine learning and clinical rules to build an algorithm for predicting ICU mortality risk. Comput Cardiol 2010;2012:401-4.
90. Lee CH, Arzeno NM, Ho JC, et al. An imputation-enhanced algorithm for ICU mortality prediction. Comput Cardiol 2010;2012:253-6.
91. Metnitz B, Schaden E, Moreno R, et al. Austrian validation and customization of the SAPS 3 admission score. Intensive Care Med 2009;35:616-22. [Crossref] [PubMed]
92. Peek N, Arts DG, Bosman RJ, et al. External validation of prognostic models for critically ill patients required substantial sample sizes. J Clin Epidemiol 2007;60:491-501. [Crossref] [PubMed]
93. Steyerberg EW, Harrell FE, Borsboom G, et al. Internal validation of predictive models: Efficiency of some procedures for logistic regression analysis. J Clin Epidemiol 2001;54:774-81. [Crossref] [PubMed]