Using linear regression to assess dose-dependent bias on a Bland-Altman plot

Assessing agreement and possible interchangeability between two methods of clinical measurement, when there is no gold standard to compare with, is common in medical research (1,2). It is well known that use of correlation coefficient or linear regression in this situation is not helpful; researchers can indeed be misguided if they conclude that the two methods of measurement are interchangeable solely because they have a highly significant statistical association (e.g., by a paired t-test) or a large correlation coefficient even when it is close to 1 (3-5).

By assessing the relationship between the differences and means of measurements derived from two methods, a Bland-Altman plot has the advantage of showing both the magnitude of bias and 95% limits of agreement between the two methods (1,4). In addition, visual inspection of the distribution of the data can also assist clinicians to determine whether the bias is constant or related to magnitude of the measurements (4). Bland and Altman have previously described that linear regression can be used to assess the relationship between bias and the magnitude of measurements (6), but the utility and limitations of such analysis have not been well described.

This viewpoint article aimed to illustrate how we can use linear regression to determine whether the bias is (I) constant or, conversely, changes with the magnitude of measurements and (II) biphasic or monophasic across the range of measurements. The factors determining the power of linear regression to detect a non-constant bias on a Bland-Altman plot will also be discussed.

Data from a recent published study assessing the agreement between measured and predicted peak oxygen consumption (pVO₂) of 43 cancer surgical patients were used to illustrate the utility of linear regression in assessing bias on a Bland-Altman plot in this study (7). Visual inspect of the Bland-Altman plot suggests that the bias (or the differences between the measured and predicted pVO₂) was not constant (Figure 1A) with the predicted pVO₂ tended to increasingly overestimate the measured pVO₂ when the means of the measured and predicted pVO₂ (on the x-axis) were increasing.

Figure 1 The relationship between the difference and mean of the measured and predicted peak oxygen consumption (pVO₂) of 43 cancer surgical patients on a Bland and Altman plot. (A) Visual inspection suggests that the predicted pVO₂ was increasingly underestimating the measured pVO₂ with increasing magnitude of pVO₂; (B) a linear regression line quantifying the differences between the measured and predicted pVO₂ increase with the magnitude of pVO₂ with a slope of −0.72 (P<0.001).

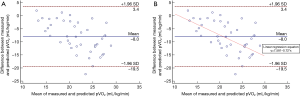
If the bias between two methods of measurement was not statistically significantly related to the magnitude of the measurements itself (the null hypothesis), then the slope of the regression line between the means and differences of the two methods of measurement would be zero. Using the difference in pVO₂ as a dependent outcome variable and the mean in pVO₂ between the two methods of measurements as an independent predictor in a linear regression, a regression line with a slope of −0.72 (P<0.001 and a nonparametric confidence interval can be obtained using unconditional bootstrap without assuming the distribution of the underlying data: www.stat.cmu.edu/~cshalizi/402/lectures/08-bootstrap/lecture-08.pdf) was obtained from the data (Figure 1B); confirming that on average, the predicted pVO₂ substantially overestimated the measured pVO₂ by 0.72 mL/kg/min (or 72%) for every mL/kg/min increment in the value of pVO2 measured.

In addition to the slope, the intercept of the linear regression equation is also important; it can help us to understand whether there is a ‘biphasic’ relationship in the bias between two methods of measurement. A ‘biphasic’ relationship suggests that one method of measurement overestimates the other when the magnitude of the measurement is large; but conversely underestimates the other when the magnitude of the measurement is small. A biphasic relationship in the bias should be suspected if according to the linear regression equation, the predicted value on the y-axis corresponding to the lowest value on the x-axis is positive but, at the same time, the predicted value on the y-axis is negative at the greatest value on the x-axis; or when the predicted value on the y-axis is negative corresponding to the lowest value on the x-axis but, at the same time, the predicted value on the y-axis is positive at the greatest value on the x-axis. In this study, the predicted value on the y-axis was −1.7 mL/kg/min at the lowest mean value (12.9 mL/kg/min) of the two measurements on the x-axis, and the value on the y-axis was −13 mL/kg/min at the largest difference between the two methods of measurement according to the linear regression line. As both y-values corresponding to the extreme low and high values on the x-axis were negative, this would suggest that the bias between the measured and predicted pVO₂ was monophasic. In other words, the predicted pVO₂ always overestimated the measured pVO₂, regardless of the magnitude of the pVO₂.

As with any statistical analyses, the power (or the ability to avoid a false negative result) of a statistical test is of pivotal importance. Based on the sample size (n=43) and standard deviation (SD) of the differences (5.8 mL/kg/min on the y-axis) and means (4.5 mL/kg/min on the x-axis) between the two methods of measurement of our study data, this dataset would have >80% statistical power to detect a relatively large linear regression slope (≥0.5 or ≤−0.5). Researchers may note that the variances or SD of the variable on the y-axis and x-axis will have an opposing effect on the statistical power of a linear regression. A smaller variance or SD of the differences between two methods of clinical measurement, or a larger variance or SD of the means between two methods of clinical measurement will both increase the statistical power of this technique (http://biostat.mc.vanderbilt.edu/wiki/Main/PowerSampleSize) to confirm whether the bias, between the two methods of clinical measurement, is constant or, conversely varies according to the magnitude of the measurement (8).

In summary, although linear regression is not helpful to assess interchangeability or agreement between two methods of clinical measurement directly, it is useful as a supplement to a standard Bland-Altman plot in assessing whether the bias between two methods of clinical measurement is constant across the range of the measurements. If bias is dose-dependent and not constant, the predicted values on y-axis corresponding to the lowest and largest values on the x-axis according to the linear regression line can inform researchers whether the bias is biphasic or monophasic. If the bias is determined to be constant according to the linear regression assessment, it will be helpful to report the magnitude of the dose-dependent bias that can be excluded with such analysis.

Acknowledgements

None.

Footnote

Conflicts of Interest: The author has no conflicts of interest to declare.

References

1. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307-10. [Crossref] [PubMed]
2. Ho KM, Joynt GM, Tan P. A comparison of central venous pressure and common iliac venous pressure in critically ill mechanically ventilated patients. Crit Care Med 1998;26:461-4. [Crossref] [PubMed]
3. Teoh PF, Seet E, Macachor J, et al. Accuracy of ProSeal™ laryngeal mask airway intracuff pressure estimation using finger palpation technique – a prospective, observational study. Anaesth Intensive Care 2012;40:467-71. [PubMed]
4. Ho KM. Scatter plot and correlation coefficient. Anaesth Intensive Care 2012;40:730-1. [PubMed]
5. Ho KM. Ten caveats of interpreting correlation coefficient in anaesthesia and intensive care research. Anaesth Intensive Care 2012;40:595-7. [PubMed]
6. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res 1999;8:135-60. [Crossref] [PubMed]
7. Li MH, Bolshinsky V, Ismail H, et al. Comparison of Duke Activity Status Index with cardiopulmonary exercise testing in cancer patients. J Anesth 2018;32:576-84. [Crossref] [PubMed]
8. Dupont WD, Plummer WD Jr. Power and sample size calculations for studies involving linear regression. Control Clin Trials 1998;19:589-601. [Crossref] [PubMed]