Importance of the baseline risk in determining sample size and power of a randomized controlled trial

Accurate estimation of adequate sample size to reduce the possibility of a type II error (false negative) is important in planning a randomized controlled trial (RCT). It becomes apparent that many recent critical care trials could not reject the null hypothesis; so much so that the proportion of clinical trials rejecting the null hypothesis on crude mortality outcome was close to the conventional acceptable type I error (5%) (1). Although it is possible that many of the tested interventions might offer no genuine treatment benefit, there are also many trial design issues that could have contributed to a low rate of rejecting the null hypothesis (or confirming the benefit of the tested intervention)—including heterogeneous study populations, expecting an unrealistically large effect size, substantial loss to follow up, and use of inappropriate outcome measures or follow up periods (1).

Baseline risk of the control group (p₁) is invariably required in the computation of the sample size of an RCT in assessing a binary outcome, as illustrated in the following formula (2).

n = the sample size in each of the groups; p₁ = proportion of subjects with mortality in the control group; * denotes multiplication; q₁ = proportion of subjects without mortality in the control group (= 1− p₁); p₂ = proportion of subjects with mortality in the treatment group; q₂ = proportion of subjects without mortality in the treatment group (= 1− p₂); X = the absolute risk reduction (ARR) the investigator expects to detect; a = conventional multiplier for alpha =0.05; and b = conventional multiplier for power =0.80.

Recent assessment of many critical care RCTs showed that the baseline risks of the control group in these trials often turned out much lower than the investigators expected (1), possibly related to the use of strict inclusion and exclusion criteria and also Hawthorne effect (because the enrolled patients were treated differently and better than the standard usual care). A reduction in baseline risk of the control group has been discarded as a major cause of inflating the type I error resulting in a false negative RCT. It is argued that a counterbalancing effect may attenuate any negative statistical effect of a lower than expected baseline risk, whereby as the baseline risk moves away from 50%, the sample size required to detect a fixed or unchanged ARR decreases (1). This argument is, however, not substantiated by common clinical sense. Treatment benefits including ARR are often dependent on severity of the illness (3). Previous studies have clearly shown that ARR of an intervention compared to the control group invariably reduces with a reduction in baseline risk for most acute medical conditions. Conversely, relative risk (RR) of an intervention is more likely to remain relatively constant across a range of severity of illness (http://archives.who.int/prioritymeds/report/annexes/4131_anx.doc) (4,5). This viewpoint article aims to illustrate how an unplanned (or unexpected) reduction in baseline risk of the control group can substantially reduce the eventual statistical power of the study often not as obvious as other problems of the trial such as loss to follow-up.

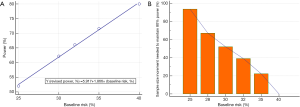
If we are planning to conduct a parallel 1:1 design RCT to assess the mortality effect of an intervention that has an expected benefit of 8% ARR, the baseline mortality rate of the control group is 40%, and assuming >80% power and an α-error <5% as acceptable, we will need 564 patients per group without factoring in the proportion loss to follow-up (Power and Sample Size Calculations software, PS version 3.1.2, 2014) (6). As we can see in the shaded boxes in Table 1, a reduction in baseline mortality rates in the control group will have a dramatic effect on the statistical power of the study (Figure 1A) to detect a relatively small absolute reduction in ARR while holding RR associated with the intervention constant.

Figure 1 Effects of an unexpected reduction in baseline risk of the control group in a randomized controlled trial. (A) a proportional loss in statistical power with a reduction in baseline risk of the control group; (B) a substantial increase in sample size is needed to counteract the effect of an unexpected reduction in baseline risk of the control group.

Table 1 Changes in statistical power with an expected reduction in baseline risk of the control group
Full table

Increasing sample size to counteract the loss of statistical power due to loss to follow-up is a common practice, but factoring in the loss of statistical power due to a smaller than expected baseline risk has not been widely promoted in RCTs. This may be due to the fact that many researchers have assumed that ARR is a “constant” attribute of an intervention, and are not aware that ARR of an intervention can significantly change with the severity of illness of the patients (as reflected by the baseline risk of the control group) with acute medical conditions (3-5). Because ARR may vary with the baseline risk of the control group, pooling RRs (or risk ratios) may also be more preferable than ARR (or risk difference) in meta-analyses when the baseline risks of the control group of the included RCTs vary substantially (7). Indeed, in order to maintain statistical power with an unexpected reduction in baseline risk in the control group, a considerable increase in sample size may be needed—perhaps much more than many researchers would have imagined (Figure 1B). As such, researchers should not assume the baseline risk of the study population as not important, or just take a Laissez-faire approach to choose an arbitrary baseline risk without due consideration.

In summary, researchers should not assume ARR as a constant attribute of an intervention especially for acute medical conditions. ARR may indeed vary significantly with the severity of illness and, hence, the baseline risk of the control group which will substantially compromise the statistical power of the study if this factor is not considered in the sample size calculation of the trial. When the baseline risk of the control group in a planned RCT cannot be determined accurately, an increase in sample size allowing up to 20% relative reduction in the baseline risk in the control group may be advisable to avoid under powering the study when the baseline risk is eventually confirmed to be lower than expected at the end of the trial. If the baseline risk of the control group turns out to be as planned, any increase in sample size to mitigate this risk will still benefit the trial by maximizing the trial’s ability to detect a smaller than expected ARR and counteract a larger proportion of patients lost to follow-up than expected.

Acknowledgements

None.

Footnote

Conflicts of Interest: The author has no conflicts of interest to declare.

References

1. Harhay MO, Wagner J, Ratcliffe SJ, et al. Outcomes and statistical power in adult critical care randomized trials. Am J Respir Crit Care Med 2014;189:1469-78. [Crossref] [PubMed]
2. Noordzij M, Tripepi G, Dekker FW, et al. Sample size calculations: basic principles and common pitfalls. Nephrol Dial Transplant 2010;25:1388-93. [Crossref] [PubMed]
3. Ho KM, Tan JA. Use of L'Abbé and pooled calibration plots to assess the relationship between severity of illness and effectiveness in studies of corticosteroids for severe sepsis. Br J Anaesth 2011;106:528-36. [Crossref] [PubMed]
4. Akobeng AK. Understanding measures of treatment effect in clinical trials. Arch Dis Child 2005;90:54-6. [Crossref] [PubMed]
5. Kent DM, Nelson J, Dahabreh IJ, et al. Risk and treatment effect heterogeneity: re-analysis of individual participant data from 32 large clinical trials. Int J Epidemiol 2016;45:2075-88. [PubMed]
6. Dupont WD, Plummer WD Jr. Power and sample size calculations. A review and computer program. Control Clin Trials 1990;11:116-28. [Crossref] [PubMed]
7. Deeks JJ. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Stat Med 2002;21:1575-600. [Crossref] [PubMed]