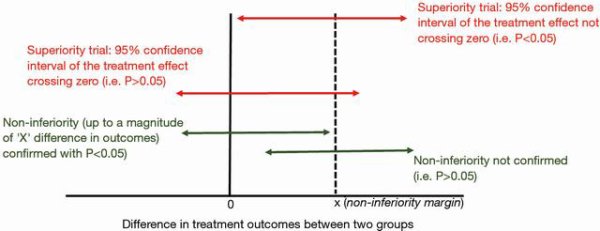
Randomized controlled trials (RCTs) are the cornerstone of evidence based medicine and are often considered the most important piece of evidence to guide clinical practice. To make sure RCTs are fit for their purpose, the design of such trials must be both statistically robust and clinically relevant. The sample size and statistical power of a study are mathematically related; it is widely accepted that the sample size should be sufficiently large to ensure a power of 80% or greater to avoid initiating a study that is destined to fail in rejecting the null hypothesis. In general, the predicted incidence of the primary outcome (in the control group) and the effect size (conferred by the test intervention) are the two most important elements that determine the mathematical relationship between sample size and the power of the study.